


How much power will we need to fly? If one fires a bullet with a mass, m, and a velocity, v, the energy given to the bullet is simply ½mv2. Likewise, the energy given to the air by the wing is proportional to the amount of air diverted down times the vertical velocity squared of that diverted air. We have already stated that the lift of a wing is proportional to the amount of air diverted times the vertical velocity of that air. Thus, the power needed to lift the airplane is proportional to the load (or weight) times the vertical velocity of the air. If the speed of the plane is doubled, the amount of air diverted down also doubles. Thus to maintain a constant lift, the angle of attack must be reduced to give a vertical velocity that is half the original. The power required for lift has been cut in half. This shows that the power required for lift becomes less as the airplane's speed increases. In fact, we have shown that this power to create lift is proportional to 1/speed of the plane.
But, we all know that to go faster (in cruise) we must apply more power. So there must be more to power than the power required for lift. The power associated with lift is often called the "induced" power. Power is also needed to overcome what is called "parasite" drag, which is the drag associated with moving the wheels, struts, antenna, etc. through the air. The energy the airplane imparts to an air molecule on impact is proportional to the speed2 (from ½mv2). The number of molecules struck per time is proportional to the speed. The faster one goes the higher the rate of impacts. Thus the parasite power required to overcome parasite drag increases as the speed3.Figure 14 shows the "power curves" for induced power, parasite power, and total power (the sum of induced power and parasite power). Again, the induced power goes as 1/speed and the parasite power goes as the speed3. At low speed the power requirements of flight are dominated by the induced power. The slower one flies the less air is diverted and thus the angle of attack must be increased to increase the vertical velocity of that air. Pilots practice flying on the "backside of the power curve" so that they recognize that the angle of attack and the power required to stay in the air at very low speeds are considerable.
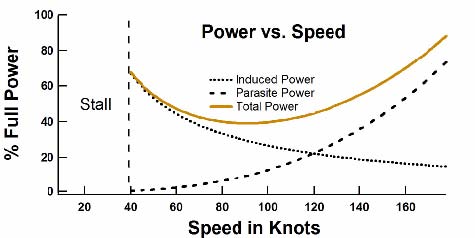 Figure 14. The power required for flight as a function of speed
Figure 14. The power required for flight as a function of speedAt cruise, the power requirement is dominated by parasite power. Since this goes as the speed3
an increase in engine size gives one a faster rate of climb but does
little to improve the cruise speed of the plane. Doubling the size of
the engine will only increase the cruise speed by about 25%.
Since we now know how the power requirements vary with speed, we can understand drag, which is a force. Drag is simply power divided by speed. Figure 14 shows the induced, parasite, and total drag as a function of speed. Here the induced drag varies as 1/speed2 and parasite drag varies as the speed2. Taking a look at these figures one can deduce a few things about how airplanes are designed. Slower airplanes, such as gliders, are designed to minimize induced power, which dominates at lower speeds. Faster propeller-driven airplanes are more concerned with parasite power, and jets are dominated by parasite drag. (This distinction is outside of the scope of this article.)
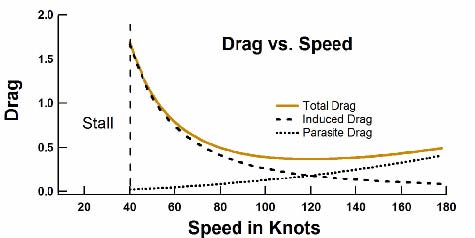
Figure 15. Drag as a function of speed
MORE (Wing Efficiency)
David Anderson,
Scott Eberhardt
How airplanes fly
Newton’s laws+lift
Air bending
Angle of attack
Air “scoop”
Lift requires power
Wing efficiency
Wing loading
Wing vortices
Ground effect
Conclusions
[HOME] [AVIATION] [How Airplanes fly] [History] [Records] [Humor] [News] [Photos] [Stories] [Stamps] [Sounds] [Movies] [HUMANS] [ORIGINS] [SCIENCE] [WEB LINKS] [SITE MAP] [CONTACT]