


One way to measure the total power is to look at the rate of fuel consumption. Figure 16 shows the fuel consumption versus gross weight for a large transport airplane traveling at a constant speed (obtained from actual data). Since the speed is constant the change in fuel consumption is due to the change in induced power. The data are fitted by a constant (parasite power) and a term that goes as the load2. This second term is just what was predicted in our Newtonian discussion of the effect of load on induced power.
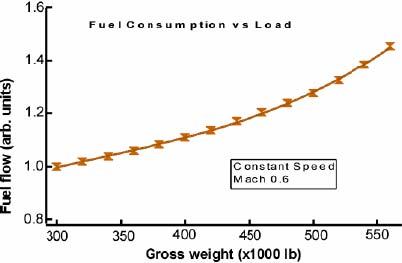
Figure 16. Fuel consumption as a function of weight for large jet at a costant speed
The increase in the angle of attack with increased load has a downside other than just the need for more power. As shown in Figure 12 a wing will eventually stall when the air can no longer follow the upper surface. That is, when the critical angle is reached. Figure 17 shows the angle of attack as a function of airspeed for a fixed load and for a 2-g turn. The angle of attack at which the plane stalls is constant and is not a function of wing loading. The angle of attack increases as the load and the stall speed increases as the square root of the load. Thus, increasing the load in a 2-g turn increases the speed at which the wing will stall by 40%. An increase in altitude will further increase the angle of attack in a 2-g turn. This is why pilots practice "accelerated stalls" which illustrates that an airplane can stall at any speed, since for any speed there is a load that will induce a stall.
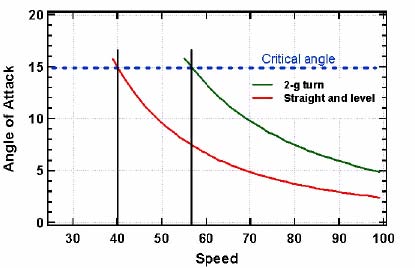
Figure 17. Angle of attack versus speed for straight and level flight and for a 2-g turn
MORE (Wing Vortices)
David Anderson,
Scott Eberhardt
[HOME] [AVIATION] [How Airplanes fly] [History] [Records] [Humor] [News] [Photos] [Stories] [Stamps] [Sounds] [Movies] [HUMANS] [ORIGINS] [SCIENCE] [WEB LINKS] [SITE MAP] [CONTACT]